默克尔树（Merkle tree）的概念由瑞夫·默克尔于 1979 年申请专利，故此得名。

Merkle tree 是一种二叉树数据结构，每个叶节点存储数据块的哈希值，而除了叶节点以外的节点存储其两个子节点值的哈希（对两个哈希值拼接后再做哈希）。哈希树能够高效、安全地验证大型数据结构的内容。

场景

假如有1000个数据块，每个块1M字节，需要用哈希值（校验码）来保证每一个数据块在传输中没有改动。 这时候有两种方案：

1. 在传输时候，增加1000个哈希值， 每个数据块对应一个。数据接收方可以用哈希值一对一分别验证各个数据块是否有改动。
2. 把这1000个块合并起来，生成一个1G的大数据块， 然后对这个1G的块做一次哈希。 数据接收方可以通过哈希值来整体上验证1000个数据块是不是有改动。

以上两个方案都有弊端：

• 方案1， 需要增加传输的数据长度。 假设用SHA256做哈希， 方案一需要额外增加 999 个 32 字节长的哈希值。
• 方案2， 只需要增加32字节的校验码（哈希值），比较高效。 但问题是，当数据接收方只想检查一个数据块的时候， 它必须得到所有的1000个数据块，拼接后统一计算才能验证。

Merkle Tree提供了第三种方案。

解决方案

Merkle Tree把数据块分别做哈希（类似上面的方案1），但并不直接传输这一堆的哈希值。 而是把这些哈希值两两拼接之后再哈希。 类似世界杯比赛一样， 直到得到最终的一个哈希值，称之为Merkle Root。 然后将所有数据块和Merkle Root的值一起传输。

接收方收到所有的数据块和Merkle Root值。 按照上述算法，可以再算一遍，验证Merkle Root是否和对数据块做Merkle哈希后的值一致。

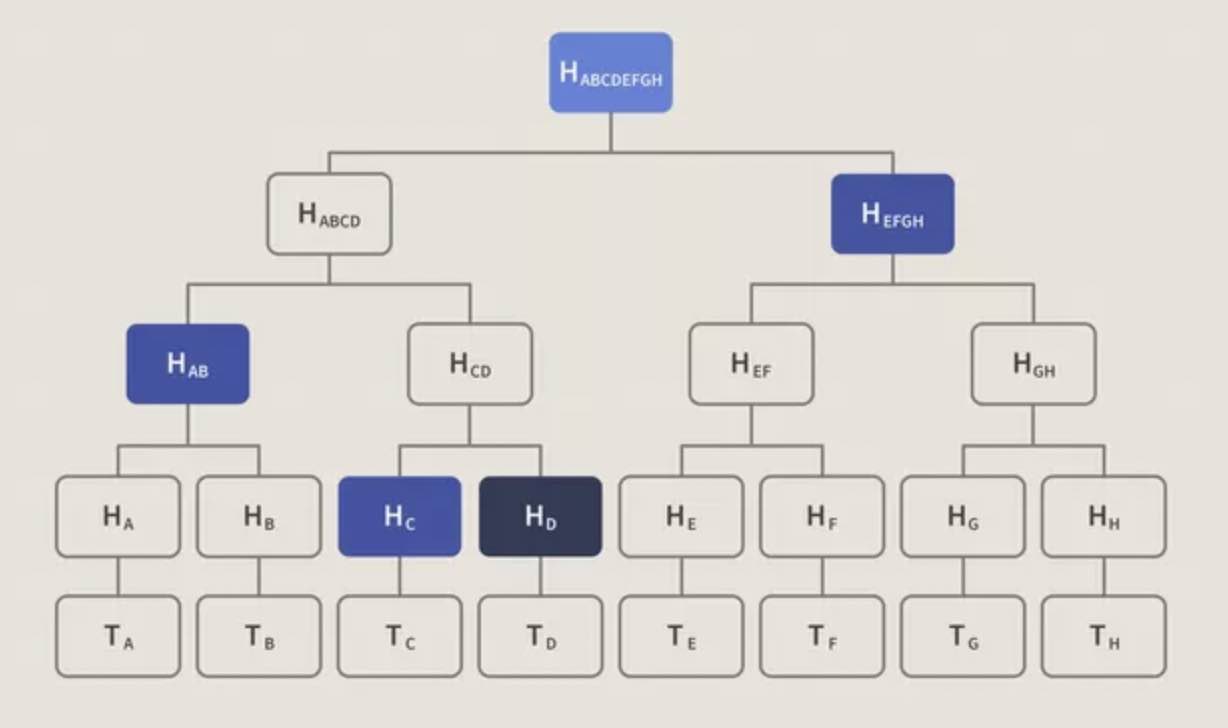
接收方如果只想验证一个数据块的完整性。 例如上图比特币中的例子，接收方只想知道交易T(D)是不是在当前区块里面， 那么它只需要得到H(C)，H(AB)，H(EFGH)和Merkle Root四个哈希值就可以验证了。当数据块越多， Merkle Tree的层级就越多。验证一个数据块，需要得到从根节点到该块所在叶子结点的树枝上的所有兄弟节点的哈希值。哈希值一般只有32字节，比交易块短的多。

在比特币中 SPV 节点就是利用Merkle Tree的这一个性质来优化和可信节点之间的交互，大大减少数据传输。

SPV 结点为什么不直接向信任的结点要求 H(D) 的值做验证？ 因为H(D)可能被伪造。 而Merkle Root的值在区块链的当前区块Header中有保存，是有完整性保护的。最终和Merkle Root做比较来验证更可靠。由于哈希函数的单向性，恶意节点无法根据Merkle Root伪造树枝上的哈希值，技术上拼不出来（需要解哈希碰撞问题）。

案例

Merkle Tree的使用场景是在分布式系统中，对数据做高效的验证时候。已经被业界广泛采用。以下是几个代表：

1. 版本管理工具 git
2. P2P浏览器 Tor
3. 区块链相关：比特币，以太坊，Filecoin等

参考资料

• Merkle Tree - Wikipedia
• Merkel Tree - Investopedia